线性规划简介
线性规划是数学规划中起源较早,应用广泛,而且方法较为成熟的一个领域。线性规划问题的目标函数 是一线性函数,所有约束条件(包括等式和不等式约束条件)也都是线性的。线性规划问题通常可以用如下 形式表达:
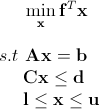
上式中fTx为目标函数,Ax=b为等式约束条件,Cx≤d为不等式约束条件, l和u分别为x的下限和上限。 满足所有约束条件(包括上下限)的点的集合是该问题的可行域。线性规划问题的 可行域如果非空的话则是一个多面体。由于线性函数是凸函数,因此线性规划问题的目标函数是凸函数,可行域也是一个凸集,因此, 线性规划问题的任意一个局域最优解都是全局最优解。
以上形式的线性规划问题在求解之前通常先被转换为标准型的问题。标准型的线性规划问题形式如下:

|
(1) |
上式中f和x为n维向量,b为m维向量,A为m乘n的矩阵。其他形式的线性规划问题都可以 通过比较简单的方法转换成以上形式。比如对于如下问题:
 , ,
|
(2) |
我们可以通过增加变量的方式将不等式约束条件转换成等式约束条件:
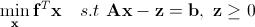
上式和标准型还是有些不同,区别在于上式中并非所有的变量都被约束为非负。这可以通过把x划分成非负和非正 两部分来解决,即
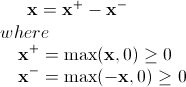
这样式(2)可改写成

很明显上式和式(1)形式一致。以下我们讲述如何求解式(1)。
在以下的分析中,我们假定式(1)中矩阵A的行数小于列数,即m<n,否则,等式约束条件就唯一确定了x 或导致问题无解,或者式等式约束条件中有冗余信息。
式(1)的拉格朗日函数为
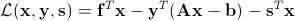 , ,
|
(3) |
通过对拉格朗日函数求偏导数,可以得到式(1)最优点的一阶必要条件:
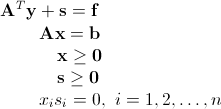 , ,
|
(4) |
以上条件同时也是以下问题的最优点的一阶必要条件:
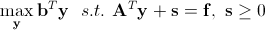 , ,
|
(5) |
式(5)正是式(1)的对偶型,式(1)也经常被称为式(5)的原始型。关于原始型和对偶型有以下理论:
- 如果原型和对偶型中的任何一个有最优解,且最优目标值有限,则另一个也有最优解,且最优目标值相同。
- 如果原型和对偶型中的任何一个的最优目标值为无穷,则另一个的可行域为空。
目前比较流行的求解线性规划问题的有单纯形法和内点法。单纯形法起源稍早,用于求解小规模的问题效果非常好。 但是,单纯形法的最坏情况复杂度为指数时间。虽然单纯形法通常远远快于其最坏情况复杂度,这还是促使了很多 科研人员寻找更为高效的算法。内点法被证明其最坏情况复杂度为多项式时间,但最初的内点法的实现方式使它的 实际复杂度经常接近其理论最坏复杂度。经过诸多科研工作者的努力改进,其效率不但提高。如今,内点法已经 成为求解大规模线性规划问题的首选。此外内点法也可以用于求解二次规划问题,而单纯形法仅能求解线性规划问题。 以下我们重点讲述用内点法求解线性规划问题。
为讲述方便,我们对式(4)稍作修改写成如下形式:
 , ,
|
(6.1) |
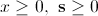 , ,
|
(6.2) |
式(6.1)中e为所有元素均为1的n维向量,X和S均为对角矩阵,且其对角线元素分别为向量x 和s中的元素,即

式(6.1)实际上是一个非线性方程组。内点法就是以牛顿迭代法的变种来求解这一非线性方程组。 内点法在迭代的过程中保持每次迭代的结果(xk, yk, sk)均严格 满足(6.2),即
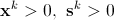
这也是内点法这一名称的由来。牛顿迭代的每一步通过计算牛顿步来修正当前的结果。牛顿步是通过求解如下线性 方程组来获得的:
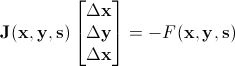
|
(7) |
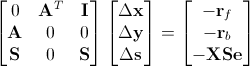
若设

则式(7)可具体化成
|
(8) |
通常在用上式求得的方向走一整步会导致(6.2)不能满足,为克服这一问题,我们可以用下式求新得迭代结果:
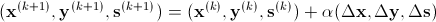
|
(9) |
上式中α为大于0小于等于1的实数。如果用纯的牛顿步,则α通常只能取很小的值,这样每一次 迭代的效果并不明显。由于这一原因,内点法对纯的牛顿迭代作了如下重要改动:

|
(10) |
式(10)中
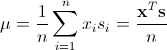
而σ则是一大于0小于1的实数。μ常被称作对偶值(duality measure),σ则常被称做趋中参数(centering parameter)。
式(10)可以通过块高斯消元消去Δs:
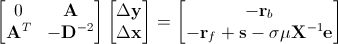
|
(11) |
上式中

式(11)可以继续通过块高斯消元消去Δx:
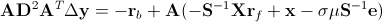
|
(12.1) |
由式(12.1)得出Δy后,Δs和Δx可由如下两式求得:
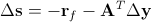 , ,
|
(12.2) |
 , ,
|
(12.3) |
得到(Δx, Δy, Δs)后就可用式(9)计算新的迭代结果,如此反复,直到达到收敛要求。
